포스팅 설명Posting Description
이 포스팅은 다국어 IT정보사이트 인포큐(InfoQ)에 게재된 2018년 7월 6일자 기고문 “Cats, Qubits, and Teleportation: The Spooky World of Quantum Algorithms (Part 2)” 전문을 저자 및 편집부 승인 하에 번역 게재한 것입니다. 기고문은 3회에 걸쳐 연재됐고 이 글은 그 두번째를 번역한 것입니다. 첫번째 번역 포스팅을 먼저 읽고 와 주시길 권합니다. 원문의 저자 홀리 커민스Holly Cummins는 2001년부터 자바 엔지니어로 활동했으며, IBM 블루믹스 거라지BlueMix Garage 테크니컬 리드를 맡고 있습니다. 그를 트위터(@holly_cummins)에서 팔로 할 수 있습니다.
저작권Copyright
※ 이 한국어 번역문의 영어판 원문을 인포Q 웹사이트에서 읽을 수 있습니다. 번역문과 원문의 일부 또는 전부를 허가 없이 복사 및 전재할 수 없습니다.
※ You can read the original article in the infoQ website. You can’t copy and publish a part or whole of this translated and the original article without permission.
핵심요약Key Takeaways
- 순간이동teleportation은 초기에 설명된 양자 정보 처리방식 중 하나다. 이는 얽힘을 이용해 먼 거리에 정보를 (이를테면) 순간적으로 전송한다.transmit 그 명칭과는 달리, 사람이나 고양이같은 큰 물체를 전송하는 데 쓰일 수는 없다.
- 양자정보이론은 사람들이 양자 시스템의 계산 복잡성the computational complexity이 실은 공개키암호public key cryptography에 쓰이는 인수분해factorization같은 다른 문제에 적용될 수 있는 계산 능력a computational capacity이었다는 점을 알아차리면서 제대로 주목받게 됐다.
- 쇼어의 로그 알고리즘Shor’s logarithms logarithms은 암호 분야를 죽이지 않는다. 이미 “양자안전quantum-safe” 암호 프로토콜이 개발됐다.
- 쇼어의 알고리즘은 첫번째 양자 ‘킬러 앱’이었다. 두번째는 2년뒤 등장한 그로버의 검색Grover’s search 알고리즘이었다. 그로버의 알고리즘은 정렬되지 않은 데이터베이스를 선형시간O(n)time 내 검색케 해준다.
- 지난 몇년새 양자컴퓨팅과 머신러닝 두 분야가 뜨겁게 달아오른만큼, 이들이 결합될 수 있을지 묻는 건 자연스럽다. 그 답은, 현재까지는, 잠정적인 ‘그렇다’로 보인다.
양자컴퓨터가 왜 흥미로운지 이해하려면, 그간 잘 알려지지 않았던 복잡성complexity 이론을 (간단히!) 들려 줄 필요가 있다. 이건 우리 대다수에게 일상생활과 거리가 멀게 느껴질 테지만, 복잡성 이론은 그저 대학교 강좌나 취업 면접시 화이트보드를 위한 것만은 아니다. 양자컴퓨팅을 그토록 빠르게 만드는 것은 양자컴퓨터의 (느린) 처리속도 또는 (터무니없이 작은) 그 컴퓨터의 메모리가 아니다. 그보다는, 알고리즘이다. 양자컴퓨터는 고전적인 대응물에 견줄 때 완전히 다른 복잡성 형질characteristics을 갖춘 새 알고리즘을 실현한다.
복잡성 연구 종사자들은 문제problems를 복잡성 계층classes으로 분류한다. 어떤 문제는 여러 계층에 속할 수 있고, 때로는 복잡성 동물원zoo이라 불릴 정도로 많은 복잡성 계층이 존재한다. 다행히 알아야 하는 건 그중 몇 개 뿐이다. NP-하드NP-hard 문제는 그 이름에서 알 수 있듯 풀기 어렵다. 해법에서 다루는 사물(수digits나, 점points이나, 도시cities)의 수가 늘어남에 따라 경악스럽게 풀기 어려워진다. NP-완전NP-complete 문제는 NP-하드 문제인데, 그 해법은 다른 NP-하드 문제를 풀게끔 일반화될 수 있다. NP-완전 문제의 효율적인 알고리즘은 복잡성 이론의 성배holy grail다. (여러분이 흥분하기 전에 미리 얘기해 두자면, 아니, 양자컴퓨팅은 이걸 제공해주지 않는다 – 아직은.)
복잡성 계층은 대문자 오 표기법big-O notation으로 정의되지만, 일반적으로, NP-하드 문제는 사물의 수를 다루는 다항식으로 척도를 삼는다scale polynomially – 즉, 20(log(n))시간 안에 풀 수 있다. 이는 점 3개에 매우 합리적인 8초를 쓰는, 점 10개에 좀 덜 합리적인 17분을 쓰는, 점 20개에 어처구니없는 12일 그리고 40개에 3만5천년을 쓰는 계산을 의미한다. 26점 계산을 끝내기 전에 그 계산을 수행하는 하드웨어 수명이 다할 테고, 31점 계산의 경우 그 프로그램을 누가 작성했든 답이 나오기 전에 죽을 공산이 크다는 식으로 생각할 수도 있다.
주요 양자 알고리즘Significant quantum algorithms
순간이동Teleportation
계산 얘긴 아니지만 순간이동을 언급하지 않고 양자 정보를 논할 수 없다. 순간이동은 초기에 설명된 양자 정보 처리방식 중 하나다. 이는 얽힘을 이용해 먼 거리에 정보를 (이를테면) 순간적으로 전송한다. 그 명칭과는 달리, 사람이나 고양이같은 큰 물체를 전송하는 데 쓰일 수는 없다. 오직 입자 하나에 적용되며, 실제 입자를 전송하는 것이 아니라 그 상태에 관한 정보만을 전송한다. 하지만 입자의 온전한 큐비트-스러운qubit-rich 상태를 전달할 수 있어, 양자 상태에 관심을 갖는 이들을 매우 흥분하게 만들었다. 양자 정보는 고전적인 채널을 통해 전송될 수 없는데, 어떤 고전적인 양자 상태 측정 행위든 그걸 교란시키기disrupts (‘붕괴시키기collapse‘) 때문이다.
양자 정보는 복사될 수 없어서, (복제불가정리the ‘no-cloning’ theorem) 입자의 정보를 원격으로 보내는 일이 원래 입자의 상태를 파괴해버리는데, 이게 아마도 ‘순간이동’이라는 이름에 영감을 줬을 듯하다. 그럼에도 중요한 건 한 장소에서 해체되고 다른 장소에서 재생성되는 게 입자가 아니라 정보라는 점이다.
아인슈타인의 특수상대성이론은 정보를 빛보다 빠르게 보낼 수 없다고 주장한다. 순간이동은 이걸 실제로 위배하진 않지만, 단지 (흥미로울만치 거의) 그런 것처럼 보인다. 광자 한 쌍이 얽히려면 같은 장소에서 출발해 서로 멀리 보내져야 한다. 이는 ‘숨은’ 정보가 빛의 속도보다 느리게 이동함을 뜻하고, 결국 아인슈타인의 이론을 따른다는 얘기다. 이건 약간 전서구carrier pigeon를 통한 통신같기도 하다. 비둘기는 말을 탄 사람보다 훨씬 빠르게 서신을 전달할 수 있지만, 말이 그 비둘기를 목적지로 실어 보내야 거기서 서신을 매단 비둘기를 집으로 돌려보낼 수 있다. (그저 확률을 측정한 결과보다) 유용한 정보를 전송하려면, 순간이동 프로토콜은 고전적인 통신 또한 요구한다 – 즉, 말이 전서구를 옮기고 나면, 두번째 말이 비둘기의 다리에 묶인 메시지를 읽는 방법을 지시하는 내용을 갖고 다른 방향으로 따라가야 한다. 이는 가까운 미래에 양자 순간이동이 초단타매매high frequency trading용으로 쓰이진 않을 듯하다는 뜻이다. 하지만 온전한 양자 정보를 붕괴시키지 않고 전송할 효과적인 방법이 있다.
양자시스템 시뮬레이션Simulation of quantum systems
놀라운 일은 양자컴퓨터같은 양자시스템을 다른 양자시스템 모사simulate에 쓸 수 있다는 게 아니다. 놀라운 일은 고전적인 컴퓨터가 양자시스템을 모사하는 데 매우 형편없다는 점이다. 작은 양자시스템은 괜찮지만 거대한 양자시스템을 효과적으로 모사하기란 불가능하다. 양자 상태 정보의 풍부함richness은 그걸 모사하기에 필요한 요소의 수가 지수적으로exponentially 늘어남을 의미한다. 리처드 파인만은 양자시스템이 훗날 양자정보이론 개발의 토대를 이룬, 심각하게 높은 계산 복잡성을 지녔음을 처음으로 알아차린 인물이다.
인수분해Factorization
양자정보이론은 양자 시스템의 계산 복잡성이 실은 공개키암호에 쓰이는 인수분해같은 다른 문제에 적용될 수 있는 계산 능력이었다는 점을 알아차린 사람들에게 비로소 주목받게 됐다. 인수분해는 주어진 수를 만들기 위해 곱해야 하는 두 수를 찾아내는 문제다. 인수분해가 때로는 흥미로운만큼 유용하지만, 흥미로운 주된 이유는 그게 어렵고, 비대칭적으로asymmetrically 어렵기 때문이다. 인수분해는 일방향함수a one-way function라 알려진 것의 한 예다. 두 제수divisors가 알려져 있다면 이를 곱한 값을 구하긴 쉽지만, 곱한 값을 갖고 그 제수를 구하려면 시간이 오래 걸린다. 인수분해된 가장 큰 숫자는 232자리 수였는데 이는 사실 그리 큰 게 아니다. (비교해 보면 파이pi는 적어도 5조자리까지 계산됐다.) 232자리 숫자 인수분해만으로도 큰 작업이었다. 수백대 머신을 썼고, 연구자들이 제수를 구하는 데 2년을 쏟았다.
이 비대칭적 어려움은 인수분해를 (예를 들자면, RSA같은) 공개키암호에 유용하게 해준다. 두 소수primes의 곱은 공개키를 만드는 데 쓰이고, 공개키는 메시지를 보내는 사람이 암호화할 때 쓰인다. 받는 사람은 원래의 인수 중 하나에 기반한 그들의 개인키를 사용해 메시지를 복호화한다. 복호화는 그 원래의 제수 하나를 안다면 쉽지만 그게 없으면 풀기 어려운 문제다.
수학적으로 증명되진 않았지만 일반사례 인수분해 문제의 고전적인 난도는 보통 그 자리수에 비례한다고 여겨지며 그건 다항식보다는 어렵지만, 지수보다는 쉽다는 얘기다. 이는 불완전 지수sub-exponential라고 알려진 것이고, 2O(n)으로 표기한다. 실제로 충분히 큰 수는 본질적으로 고전적인 수단으로는 인수분해되지 않는다.
수학자 피터 쇼어Peter Shor는 1994년 양자컴퓨터가 다항식시간내에 인수분해 문제를 푸는 데 쓰일 수 있음을 보였다. 그는 양자 계산의 이론적인 전망에 대한 얘길 들었지만, 당시 그걸 위해 유용한 알고리즘을 정의한 이는 아무도 없었다. 그는 일반 계산 문제를 푸는 양자컴퓨터를 만드는 방법을 생각하기 시작했지만, 그가 뭘 했는지 아무에게도 얘기하지 않았다. 그는 로그를 찾는 양자 알고리즘을 만들어내는 (파트타임) 작업에 1년을 쏟았다. 4일 뒤, 그는 그의 로그 알고리즘을 효율적인 인수분해 알고리즘에 적용했다.
인수분해가 대다수 공개키암호의 핵심적인 부분이었기때문에 쇼어의 작업은 곧 사람들에게 주목을 받았다. 하지만 쇼어의 알고리즘은 암호 분야를 죽이지 않는다. 이미 “양자안전” 암호 프로토콜이 개발됐다. 게다가, 이 시리즈 3편에서 보겠지만, 쇼어의 알고리즘을 제대로 구동하려면 수천 큐비트짜리 양자컴퓨터가 필요하다.
쇼어의 알고리즘은 양자 중첩을 이용해 많은 가능성possibilities을 시도해 동작한다.
하지만 쇼어의 알고리즘의 세부내용은 단지 ‘가능한 인수를 모두 시도한 다음 뭐가 맞는지 보는 것’보다 더 복잡하다. 이는 양자컴퓨터에서 수행될 수 있지만, 어떤 측정이든 임의의 – 그리고 가장 부정확할 듯한 – 인수를 내놓는다.
쇼어의 알고리즘의 영리함은 많은 가능성을 시도한 후에 모든 답에 함께 간섭해, 측정이 부정확한 답보다는 정확한 답을 얻게끔 했다는 점이다. 고전적인 컴퓨터에서 ‘답에 간섭하기Interfering answers‘란 말도 안 되는 얘기지만, 양자컴퓨터로는 양자 상태의 파동스러운wave-y 특성을 이용해 이걸 한다. 정확한 가능성을 증폭하려고 가능성에 간섭하는 게 여러 양자 알고리즘의 공통된 특징이다.
쇼어의 해법 첫 부분은 고전적인 계산을 함수의 주기the period of a function(즉, 그 파장frequency)를 찾는 계산을 하는 인수분해 문제로 환원하는 것이다. 그렇게 하면, 이 문제는 파동과 파장에 대한 것이고, 비로소 양자 파동과 간섭을 끌어들인 해법이 더 자연스럽게 느껴지기 시작한다.
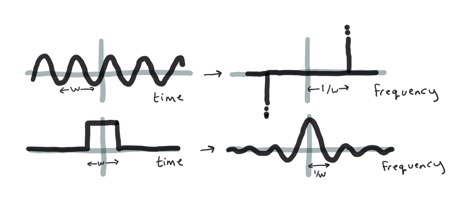
고전적인 수학에서 푸리에 변환Fourier transform은 (파 신호wave signal같은) 함수를 그 구성주파수constituent frequencies로 바꿀 때 쓰인다. 알 수 없는 함수의 푸리에 변환을 구하려면, 그 여러 점을 측정할 필요가 있는데, 그게 얼마나 자주 반복되는지 알아내야 하기 때문이다. 예를 들어 표준 사인sine파의 푸리에 변환은 (y축 주위에서 대칭하는 단일 파장뿐인) 가시 한 쌍이다. 상자 함수의 푸리에 변환은 점차 잦아드는 돌기 모양이다.
양자 푸리에 변환은 시계열timeseries을 이루는 파장을 집어내는 동일 목적을 갖고 있지만, 중첩을 이용해 한 순간에 여러 점으로 함수를 효과적으로 측정 가능하고, 그 다음 파동에 간섭해 옳은 답을 증폭시키고, 틀린 답을 사라지게cancel out 할 수 있다. 이걸 하고 나면 어떤 측정이든 그 시스템을 옳은 답으로 붕괴시킬 확률이 높다.
틀린 답이 스스로 사라지게끔 파동을 함께 섞는 건 고전적인 컴퓨터 작동 방식과 매우 다르지만, 이는 거시세계the macroscopic world에서 우리 대다수가 경험한 일이다. 예를 들어, 소음제거noise cancelling 헤드폰은 기존 노이즈에 여분의 소음을 더해 작동한다. 이는 외부 소음을 재생성한 여분의 음파를 그 위상을 옮긴 채로 재생한다. 새로운 음파가 원치 않는 소음 파동과 정확히 180도 위상차를 이뤄 완벽하게 복사되는 한, 이들은 서로를 말끔히 사라지게 하고, 착용한 사람에게 행복한 정적을 안겨 준다.
검색Search
쇼어의 알고리즘은 첫번째 양자 ‘킬러 앱’이었다. 두번째는 2년뒤 등장한 그로버의 검색Grover’s search 알고리즘이었다. 그로버의 알고리즘은 정렬되지 않은 데이터베이스를 
시간 안에 검색케 해준다. 예를 들어 이는 누군가의 전화번호만을 알고 있을 때 전화번호부에서 그의 이름을 찾는 데 쓰일 수 있다. 그로버의 알고리즘은 쇼어의 인수분해 알고리즘처럼 인상적인 속도향상을 가져오진 않았다. 지수적인 속도향상이 아니라 (말하자면, 원소의 수를 제곱근한 값에 비례하는) 이차quadratic 속도향상이었다. 그 완만한 속도향상은 그로버 알고리즘의 광범위한 응용가능성과 맞선 균형을 이룬다.
그로버가 그의 알고리즘을 데이터베이스 검색 측면으로 설명하긴 했지만, 실은 그보다 더 일반적이다. 검색 대상은 어떤 함수를 충족하는 뭔가이기만 하면 – 다시 말해 어떤 문제의 답이기만 하면 된다. (기술적으로 말하자면, 그 목표는 ‘어떤 함수의 역inverse of a function‘이다.) 그런 문제는, 예를 들어, ‘이 메시지를 복호화하는 데 쓸 수 있는 키는 뭐지?’같은 것이 될 수 있다. 다시 말해, 그로버의 검색 알고리즘은 암호를 깨는 무차별대입공격brute-force cracking의 속도향상에 쓰일 수 있다. 심지어 인수분해 기반이 아닌 암호에도 그렇다. 또 이는 숫자 세트의 일반값average (평균mean이나 중앙값median) 추정에도 쓰일 수 있다.
그로버의 알고리즘은, 다른 여러 양자알고리즘처럼, 확률적probabilistic이다. 각 실행은 옳은 답을 낼 가능성과, 틀린 답을 얻게 할 – 낮은 – 가능성을 갖는다. 이는 매우 마뜩찮아 보이지만, 실은 보기보다 훨씬 유용하다. 답이 함수의 해이기 때문에, 만일 알고리즘이 틀린 답을 낸다면 즉각적으로 알아차릴 수 있다. n개 원소 시스템에서 해를 구하려 시간을 써버렸는데 틀린 답만을 얻었다면, 꽤 우울할 것이다. 하지만, 길고 느린 계산이 여러번 반복돼야 한다면 그 해를 구하는 전체 시간은 여전히 
이고 결정적인deterministic 고전 알고리즘을 이용하는 것보다 훨씬 더 빠를 것이다. (계산이 틀릴 확률은 n과 함께 늘어나지 않고, 이는 오류 가능성이 허용되는 이유다.)
충돌Collision
그로버의 알고리즘을 일반화한 것은 ‘충돌 문제collision problems‘를 푸는 데 쓰일 수 있다. 어떤 함수를 만족하는 것 하나만을 구하는 게 아니라 같은 답을 구하기 위한 여러 원소를 찾을 수 있다는 얘기다. 공간상의 물리적 충돌, 그리고 생일이 같은 두 사람을 찾는 것과 같은 더 일반적인 문제를 이해할 때 유용하다. 그로버의 원래 알고리즘처럼, 이는 동일한 해시를 얻을 수 있는 두 숫자를 찾는 암호 공격의 기반을 구성할 수 있다(이것의 고전적 버전은 ‘생일 공격’이라는 유쾌한 이름이 있다).
외판원 문제The travelling salesman problem
양자 알고리즘은 일반적으로 모든 가능한 해를 시도한 다음 진폭 증폭amplitude amplification으로 정답이 선택되는 과정을 거치기 때문에, 양자컴퓨터는 최적화 문제optimisation problems를 풀기에 탁월할 것처럼 보인다. 현재까지 범용 양자 최적화 알고리즘은 없지만, 최적화 문제의 일부 하위범주subclasses를 푸는 흥미로운 양자 솔루션은 있다. 외판원 문제는 매우 유명한 최적화 문제 중 하나로 알려져 있다. 여러 장소를 여행해야 하는 판매원에게 가장 짧은 경로를 찾는 도전과제로 묘사된다. 장소의 수가 늘어날수록, 최적 경로 찾기의 어려움도 늘어난다. 외판원 문제는 NP-하드 문제에 해당하고 장소의 수에 지수적으로 비례한다. 판매원 문제의 정확한 해를 계산하려면 수십개 도시를 계산하는 것만으로도 몇 년(또는 수백만년)이 걸릴 수 있다.
외판원 문제는 지속적인 연구 분야다. 최근까지 가장 잘 알려진 양자 알고리즘은 (이차 속도향상의) 
이고, 가장 잘 알려진 고전적 알고리즘은 O(2n)이었다. 2017년 3월, 어떤 양자 알고리즘이 공개돼 여러 사례에서 준 이차near-quadratic 속도향상을 가져왔고, 여전히 더 많은 개선 사례가 발견될 수 있다.
머신러닝Machine Learning
지난 몇년새 양자컴퓨팅과 머신러닝 두 분야가 뜨겁게 달아오른만큼, 이들이 결합될 수 있을지 묻는 건 자연스럽다. 그 답은, 현재까지는, 잠정적인 ‘그렇다’로 보인다. 수학적인 수준에서 양자상태 계산과 머신러닝 모델 둘 다 행렬matrices에 매우 의존한다. 개념적으로, 머신러닝은 데이터에서 패턴 찾기에 가깝고, 양자계산의 간섭-및-증폭-파동 모델 또한 패턴 찾기에 잘 들어맞는다.
양자컴퓨터는 로그 리소스logarithmic resources를 이용한 행렬의 역matrix inversion과 같은 걸 다룰 수 있다(행렬의 역은 선형방정식 시스템a linear system of equations을 푸는 것과 마찬가지다). 이 행렬의 역은 다양한 머신러닝 문제에 유용하다. 더 일반적으로, 그로버의 알고리즘은 ‘올바른’ (즉, 주어진 함수를 만족하는 하나의) 답을 찾는 데 쓰일 수 있다. 군집화clustering같은 다른 머신러닝 문제는 고유한 양자 알고리즘이 있다.
양자컴퓨터는 이론적으로 (알려지지 않은 임의의 비트 열을 검사해 밝혀내는) ‘블랙박스 문제’라 알려진 것을 푸는 데 더 좋다는 것이 증명됐고, 연구자들은 5비트 블랙박스 구현을 선보였다. 또한 (원리상 충분히 거대한 컴퓨터를 이용하면) 고전적인 컴퓨터로 구동하려면 시간이 너무 오래 걸릴 시퀀스 발견이 가능할뿐아니라, 양자컴퓨터는 그 판독 중의 노이즈를 더 잘 견디기도 한다.
범용 양자 속도향상은 없다No Universal Quantum Speedup
이들 알고리즘은 모두 특정 계층의 문제를 대상으로 한다. 검색이나 외판원 문제같은 일부 알고리즘은 많은 잠재적 응용 여지가 있지만, 그 알고리즘 자체는 매우 특정적이다. 아직 ‘범용 양자 속도향상’으로 알려진 게 없다. 달리 말하자면, 복잡성 계층 관점에서 BQP는 NP와 겹친다고 알려져 있지만, 아직 그게 얼마나 많이 겹치는지는 아직 알려지지 않았다. 아마도 
일 것 같은데, 아직 증명되지 않았다. 피터 쇼어는 양자 알고리즘이 흥미로운 속도향상을 제공하려면 올바른 답에 도달하는 계산 경로를 건설적으로 간섭하고, 틀린 답으로 가는 경로를 서로 사라지게 해야 한다고 지적했다. 아직 일반화할 수 있는 틀린-경로가-서로를-없애게-만드는 프로세스는 없다. 문제가 얼마나 어려운지 고려할 때, 아마 절대로 없을 것이다.
일반 양자 알고리즘의 부재는 알려진 알고리즘이 얼마나 흥미로운지 또는 얼마나 광범위하게 적용 가능한지를 떼어놓고 볼 수 없다. 이 시리즈의 다음 기사는 이런 문제 영역 중 일부가 뭔지 논하고, 미래 양자 계산이 실현할만한 것을 들여다보겠다.
양자컴퓨팅 관련 연재의 두번째 글이다. 주제를 소개하고 양자계산에 초점을 맞춘 첫번째 글은 “고양이, 큐비트, 그리고 순간이동: 양자 연산의 이상한 세계 (1편)”에서 찾을 수 있다. 양자 애플리케이션에 초점을 맞춘 세번째 글은 “고양이, 큐비트, 그리고 순간이동: 양자 연산 애플리케이션의 이상한 세계 (3편)”에서 찾을 수 있다.
저자 소개About the Author
홀리 커민스는 풀스택 개발자, 클라우드컴퓨팅 테크니컬 리드다. 단골 강연자, 자바 챔피언, 엔터프라이즈 OSGi 인 액션의 저자이기도 하다. 이 사람은 옥스포드대학교 양자계산학 박사DPhil in Quantum Computation 학위 보유자다.
—
180801 번역 준비. 180806 번역 시리즈 포스팅 URL 형식 결정. 180827 번역 시작. 180902 30% 완료. 180909 60% 상태로 발행. 180910 일부 수정. 180911 일부 수정 및 80% 완료. 180912 완료. 181021 2편 번역판 링크 추가 및 재편집. 231105 저자 소개 문구의 ‘그는’을 성별 중립적인 ‘이 사람은’으로 수정함.