포스팅 설명Posting Description
이 포스팅은 다국어 IT정보사이트 인포큐(InfoQ)에 게재된 2018년 6월 29일자 기고문 “Cats, Qubits, and Teleportation: The Spooky World of Quantum Computation (Part One)” 전문을 저자 및 편집부 승인 하에 번역 게재한 것입니다. 원문의 저자 홀리 커민스Holly Cummins는 2017년 3월 30일 새로 지명된 자바 챔피언 3명 가운데 한 사람입니다. 이 사람은 2001년부터 자바 엔지니어로 활동했으며, IBM J9 JVM의 가비지 콜렉션GC 및 저스트인타임JIT 컴파일레이션 부분을 작업한 코어 엔지니어들 중 한 사람이기도 합니다. 현재 IBM 블루믹스 거라지BlueMix Garage 테크니컬 리드를 맡고 있습니다. 그를 트위터(@holly_cummins)에서 팔로 할 수 있습니다.
저작권Copyright
※ 이 한국어 번역문의 영어판 원문을 인포Q 웹사이트에서 읽을 수 있습니다. 번역문과 원문의 일부 또는 전부를 허가 없이 복사 및 전재할 수 없습니다.
※ You can read the original article in the infoQ website. You can’t copy and publish a part or whole of this translated and the original article without permission.
핵심요약Key Takeaways
- 20년전 양자컴퓨터는 순수 이론이었고, 오로지 화이트보드와 학술 논문상으로만 존재했다. 이제 양자컴퓨터는 클라우드에서 빌려 쓸 수 있다.
- 빛은 에너지의 불연속적 덩어리(입자) 상태로 움직이지만, 이런 덩어리는 파장frequency과 다른 파장에 간섭하는 능력과 같은 파동wave의 속성을 많이 지닌다.
- 위치position와 운동량momentum뿐아니라, 모든 양자 파동-입자-사물은 스핀spin이라는 세번째 속성을 지닌다. 측정된 스핀은 완전 위 또는 완전 아래가 되지만, 측정할 때는 위이거나 아래일 가능성을 모두 지닌다. 즉 측정되기 전까지 스핀은 위이면서 아래다. 이를 중첩superposition이라고 한다.
- 양자의 이상함 마지막은 양자 사물의 쌍(또는 군집)이 어떤 속성을 공유한다는 것이다. 이 ‘얽힘entanglement‘은 서로 1.3km 떨어져 위치한 전자 사이에서도 달성됐다.
- 양자정보이론의 최소단위인 큐비트 또한 0이나 1이 될 수 있다. 고전적인 비트와 달리 큐비트는 0과 1 상태의 결합combination이 될 수도 있다.
우리 대다수는 어른이 되면서 몇가지 기본적인 진실을 알게 된다. 고양이는 죽은 동시에 살아있을 수 없다. 우주 반대편 끝에 있는 물체들은 서로 영향을 줄 수 없다. 컴퓨터는 0과 1로 작동하고, 그게 대다수 정보의 기초 단위다. 양자 연산의 전제는 이런 진실이 부분적으로 틀렸다는 것이다. 걱정 마시라, 고양이 얘기는 대체로 맞으니까, 적어도 실제 고양이라면, 그리고 빛보다 빠르게 다닐 수 있는 건 없으니까.
20년전 양자컴퓨터는 순수 이론이었고, 오로지 화이트보드와 학술 논문상으로만 존재했다. 구현될지조차 불분명했다. 10년전부터 양자컴퓨터 구현이 진행됐지만, 실제 유용한 양자컴퓨터는 머나먼 기대였다. 이제 양자컴퓨터는 클라우드에서 빌려 쓸 수 있다. 기업, 학술단체, 정부 연구소는 전통적인 연산으로는 너무 어려운 문제를 풀 수 있는 양자컴퓨터를 처음 발표하는 경주에 뛰어들고 있다.
하지만 양자컴퓨터를 그렇게 강력하게 만드는 건 뭘까? 양자컴퓨터를 유용하게 하는 건 어떤 종류의 문제일까? 현대 양자컴퓨터는 실제로 어떻게 작동할까? 미래엔 우리 컴퓨터가 모두 양자컴퓨터가 될까?
양자역학개론Introduction to quantum mechanics
양자역학은 20세기 초입에 물리학자들이 더 작디 작은 입자를 연구하면서 개발됐다. 그들이 실험적으로 관찰한 걸 설명하기 위해 그들은 새로운 모델을 고안해야 했다. 19세기 굴절과 간섭 관찰은 과학 공동체에서 빛이 (수영장의 물결 또는 공기 중의 음파같은) 파동이었다는 일반적인 합의를 이끌어냈다. 점차 정교한 실험으로 원자가 궤도를 도는 전자electrons에 둘러싸인 양성자protons와 중성자neutrons의 고밀도 코어로 이뤄진 행성같은 내부 구조를 지녔음이 드러났다.
양자화Quantisation
빛이 파동이라는 해석은 2가지 실험적 현상을 설명해야 할 필요가 생기자 충격을 받게 됐다. 매우 뜨거운 물체가 빛을 내뿜는 방식(열복사thermal radiation), 그리고 금속에 빛을 쪼이자 전기를 내놓는 방식(광전효과the photoelectric effect). ‘정상’ 물리학 모델은 뜨거운 물체에서 고주파의 빛이 방출되는 방식을 예측하는 데 형편없었다. 막스 플랑크Max Planck는 복사 에너지radiant energy가 불연속적 덩어리로 취급된다면 이론이 현실과 들어맞을 수 있다는 점을 발견했다. 그가 자신의 연구를 출판했을 때 그는 현실의 본질에 과감한 견해를 펼칠 뜻이 없었다. 그는 자신의 발견이 그저 유용한 수학적 비결이라고만 여겼다.
아인슈타인은 광전효과를 설명할 이론을 만들었다. 그는 빛이 입자인 동시에 파동으로 간주된다면 광전효과가 깔끔하게 설명될 수 있음을 증명했다. 즉, 빛은 에너지의 불연속적 덩어리인 채로 운동하지만, 이 덩어리는 파장 그리고 다른 파장에 간섭할 수 있는 능력과 같은 파동의 속성을 많이 갖고 있다. 만일 이게 혼란스럽다면, 그럴 수밖에! 우리에게 (모래같은) 입자나, (해변에서 볼 수 있는 것 같은) 파도는 익숙하지만, 우리가 뭔가를 모래이면서 동시에 파도인 것으로 이해할 수 있게 해주는 그럴싸한 비유는 없다.
물질의 사정도 나을 게 없다. 전자는 양성자 핵을 중심으로 궤도 운동을 하지만, 이 궤도란 행성의 궤도같은 게 아니고, 대신 사다리의 가로대같은 것이다(“양자화”). 전자는 오로지 가로대 사이를 넘어다니는 것만 허용되고, 절대 그 사이 공간에 위치할 수는 없다. 여러분은 아마 “대체 어떻게 가로대와 가로대의 사이 공간을 지나치지 않고 그렇게 움직일 수 있느냐?” 물을 것이다. 많은 뛰어난 물리학자들이 정확히 같은 질문을 던졌고, 과학계 전반은 어쩌면 우리가 양자 도약quantum jumps을 만족스럽게 설명할 방법을 절대 찾지 못할 수도 있다는 체념을 수용하는 데 합의한 듯하다.
파동-입자 이중성Wave-particle duality
게다가 또 있다 – 빛이 파동이면서 입자인 것처럼, 물질 – 단단하고, 만질 수 있고, 굽이치지 않는 물질 – 조차 실은 파동이면서 입자라는 것이다. 실험을 통해 전자와 분자들이 다른 것을 회절하고 간섭하는 것이 관찰됐다. 이는 파동-입자 이중성이라 알려진 것으로, 물질과 빛 모두에 적용된다. 이는 물질과 빛이 – 비록 완전히 별개인 것처럼 보이긴 하지만 – 폭넓게 유사성을 띤다고 주장하는 더 광범위한 이론적 프레임워크의 일부다. (아인슈타인의 유명한 방정식, E = mc2, 은 이 아이디어의 연장이며, 빛과 물질이 서로 바뀔 수 있는 방식을 표현한 것이다.)
스핀Spin
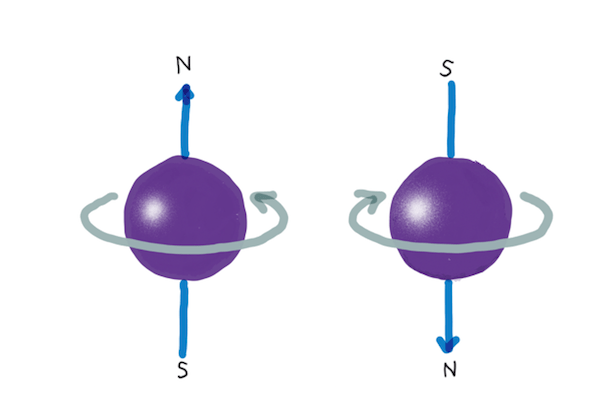
위치 및 운동량과 더불어 모든 양자 파동-입자-사물은 스핀이라는 제3의 속성을 띤다. 스핀은 자기장 안에서 마치 스스로 자석이 된 것처럼 편향하는deflected 입자를 통해 처음으로 발견됐다. 고전적인 세계에서 이는 대전된 물체charged objects가 회전할 때 발생하는 일이었기에, 최초의 실험자들은 그들이 관찰한 것을 스핀이라고 불렀다. 각운동량angular momentum에 빗댄 것이지만 양자 스핀은 일종의 은유metaphor로 봐야 한다. 만일 양자 입자가 실제로 회전한다면 (그리고 그게 실제로 입자라면), 관측되는 자기 효과magnetic effect를 달성하기 위해 그 표면은 빛보다 빠른 속도로 움직여야 한다.
스핀이 양자화된 속성이라는 게 놀랍지 않을 수도 있겠다. (계속 따라오고 있다면 이게 각운동량같은 것과 훨씬 덜 비슷하게 느껴질 거다.) 개별 입자의 스핀은 위up 아니면 아래down라는 2가지 값으로만 가능하다. 오로지 2가지 값만 성립한다는 사실은 스핀을 이 뒤에서 다룰 양자정보저장 측면에 유용한 속성으로 만들어 준다. 또 사물은 그 스핀 값이 바뀌더라도 여전히 자리잡고 있기 때문에 스핀은 양자정보로 사용하기 편리하다. 이와 달리 운동량이나 위치가 바뀌면 별로 좋지 않다. 이는 컴퓨터 내부가 끊임없이 가속하고 감속하면서 경주하도록 요구할 것이다.
중첩Superposition
선택할 수 있는 값이 2가지 뿐이라, 양자 스핀은 지루한 속성이 될 수 있다. 상당히 이상한 양자 현상 중 하나인 중첩 때문에 세상이 좀 더 활기를 띤다. 측정된 스핀은 완전 위 또는 완전 아래가 되지만, 측정할 때는 위이거나 아래일 가능성chance을 함께 지닌다. 즉 측정되기 전까지 스핀은 위이면서 아래다. 위일 경우와 아래일 경우가 얼마나 혼합돼 있느냐가 위로 측정되거나 아래로 측정될 가능성을 결정한다. 이 사실은 위치나 운동량같은 다른 관측치에도 마찬가지다. 이를 중첩이라고 한다. 측정이 되면 그 상태는 단일 지점에 수렴한다converges. (이 수렴 방식은 여전히, 측정 문제measurement problem라 알려진 과학적 논쟁의 주제다.)
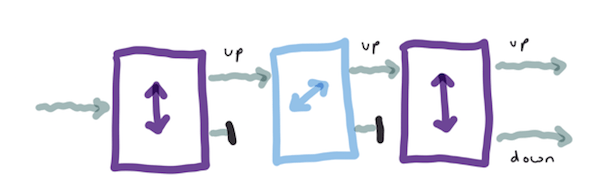
중첩 상태가 직접 관찰되지 않는데, 우리는 왜 입자가 중첩 상태에 있다고 여겨야할까? 중첩이 수학적 수준에서 파동-입자 이중성을 띠기 때문이다. 그 첫번째 증거는 어떤 측정이 명백하게 임의적인random 결과를 내놓는다는 점이다. 임의성 자체는 측정이 끝나기 직전까지 상태가 중첩돼 있었다는 증거가 아니지만, 더 강력한 실험이 있다. 양자 스핀은 자기 상자magnetic box에 뜨거운 원자의 흐름stream을 통과시킬 때 처음으로 관찰됐는데, 그 결과 원자가 (위 스핀과 아래 스핀이라는) 두 깔끔한 흐름으로 비껴가는 걸 볼 수 있었다. 흐름 중 하나만이 (이를테면, 위 스핀이) 그와 같은 방향으로 자기장이 향하는 제2의 상자를 통과하면, 흐름은 다시 나뉘지 않았다. 놀랄 일이 아니다. 우리는 위 스핀을 걸러냈고, 다시 그 스핀을 측정했으며, 그게 위 스핀을 유지하는 것이다. 제2의 상자가 회전해 그 자기장이 처음 것의 90도로 바뀌면, 스핀은 다른 축에서 측정되고, 우리는 그 축을 걸러내지 않았기 때문에, 그 흐름은 다시 둘로 나뉜다. 원래 방향으로 자기장이 향하는 제3의 상자가 추가되면 어떤 일이 벌어질까? 원자 흐름은 이미 위 스핀만을 포함하도록 걸러졌지만, 그 흐름은 나뉜다. 다른 축으로 스핀을 측정하는 일이 걸러냄을 취소한다. 이걸 달리 표현하자면, 회전한 자기장을 펼친 가운데 상자가, 원자를 중첩 상태로 되돌려 놓는다. (이 실험은 중첩을 보여줄 뿐아니라 하이젠베르크의 불확정성 원리Heisenberg’s uncertainty principle를 보여 준다. 우리는 스핀이 어떤 방향인지 알면 다른 방향의 스핀에 대한 지식을 지워버린다.)
양자 이론은 반직관적인데, 왜냐면 우리는 모두 세계가 그렇게 작동하지 않는다는 걸 알기 때문이다. 이론은 심지어 그걸 개발한, 그 이상한 함의로 고생하는 과학자들에게조차 정착되지 않았다. 아인슈타인Einstein은 세계가 근본적으로 비결정론적이라는 생각을 싫어했고, ‘신은 주사위놀이를 하지 않는다God does not play dice‘는 유명한 표현을 하게 만들었다. 슈뢰딩거Schrödinger는 그가 ‘양자도약 난센스the quantum jump nonsense‘라 부른 걸 그의 후기 이론 연구에서 제외하고자 했고 그제껏 양자이론에 공헌해온 것에 후회를 표했다.
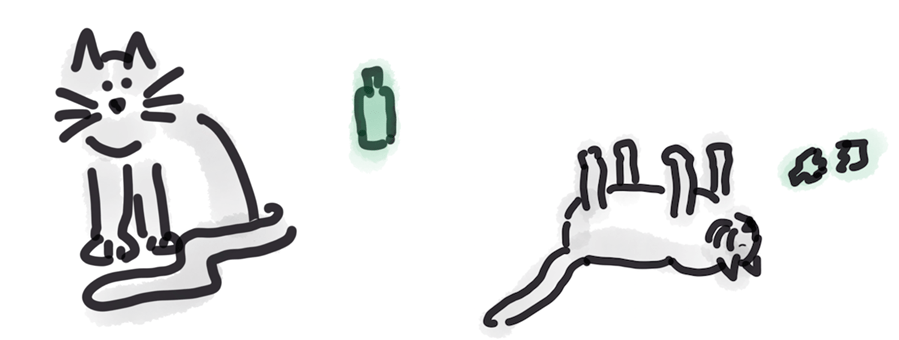
슈뢰딩거는 중첩이 얼마나 부조리한지 보여주기위해 바깥 세계와 격리된 상자 속 고양이를 둔 사고 실험을 고안했다. 상자 안에는 방사성 암석, 시안화합물 병, 방사능이 검출되면 병을 부수는 망치와 연결된 가이거 계수기가 같이 들어 있다. 방사능선원radioactive source으로부터 방출되는 입자는 (방사능은) 사전 예측할 수 없는 확률적 사건이다. 입자가 방출되면 독이 흘러나와 상자의 고양이를 죽인다. 양자 이론은 측정이 실행되기 전까지 자연 붕괴되는 입자가 붕괴된 상태와 붕괴되지 않은 두 상태 모두에 해당한다고 말한다. 이는 누군가 저 고양이의 생존을 확인(‘측정’)하려고 그 상자 안을 들여다볼 때까지는 이 고양이가 동시에 살아 있으면서 죽어 있을 것이란 뜻이다. 모두가 고양이는 동시에 살아있으면서 죽어있을 수는 없다는 슈뢰딩거에게 동의했지만, 중첩이 실험적 증거에 가장 잘 맞는 이론이라는 점을 부인할 수 없었다. 이는 어떤 이론이 정확한 동시에 완전히 부조리할 수 있느냐는 흥미로운 도전을 이끌어냈다.
슈뢰딩거의 고양이는 2가지 이유로 사고 실험에 머물러 있다. 첫째로 이는 실제 실험으로 구성하기가 불가능해 보이기 때문이다. 관찰하는 것 외에 고양이의 상태를 알 수 있는 실험자는 없었고, 고양이의 생사를 측정하는 건 그 자체가 양자 붕괴를 촉발하는 행위였다. 둘째로 물리학자가 상자에 고양이를 가둔 채 그걸 확률적으로 독살하는 건 비윤리적이라는 이유에서다.
얽힘Entanglement
양자의 기괴함을 보여주는 마지막 조각은 양자적 사물의 쌍(또는 그룹)이 공유 속성을 지닐 때 발생한다. 예를 들어 광자를 분할해 광자 한 쌍이 생성될 경우, 생성된 한 쌍의 전체 스핀은 원래 광자의 스핀과 같아야 한다. 중첩이 개입해서 측정된 상태는 측정되는 시점에만 결정된다는 점을 제외하면, 여기까지는 훌륭하다. 광자 한 개의 상태를 알게 되면 우리는 다른 광자의 상태가 뭔지도 정확하게 알 수 있다. 말인즉, 이 쌍의 한 쪽이 측정돼 그 상태가 붕괴하면collapses, 다른 광자의 상태도 바로 그 순간 붕괴한다.
[역자주] 영어로 ‘붕괴한다’는 표현이 방사성동위원소의 붕괴와 같은 단어로 쓰이긴 했지만, 실제 의미는 측정이전에 가능했던 양자적 사물의 상태를 나타내는 확률분포 그래프가 특정한 측정결과 값으로 수렴한다는 것을 의미. 도표의 그래프로 퍼져있던 확률이 현실의 측정값으로 결정되는 것도 양자역학에서 ‘붕괴한다’고 표현. 이 문맥상 적절한 한국어 표현이 없음.
아인슈타인은 정보는 빛보다 빠르게 움직일 수 없음을 선언한 걸로 유명하니, 그가 이런 ‘원거리의 이상한 행동spooky action at a distance‘이라 묘사한 것에 불쾌해 한 것은 이해할만한 일이었다. 그는 멀리 떨어진 거리에 있는 사물이 동시에 서로의 상태에 영향을 줄 수 없어야 한다고 생각했다. 이 문제를 풀기 위해 물리학자들은 ‘숨은 변수hidden variable‘ 이론을 제시했다. 상태가 완전히 임의적으로 보였더라도 측정할 수 없는 다른 속성이 있다는 가정을 통해, 실은 측정 결과가 항상 결정돼 있었고, 따라서 빛보다 더 빠른 정보전달 효과라는 고민거리는 없다고 보는 것이다. (정의상 변수가 숨어 있다는) 숨은 변수 이론을 반박하기는 어려워 보인다. 하지만 숨은 변수가 처음 제안된지 30년이 지난 뒤 존 벨John Bell은 여러 다른 축을 따라 측정을 수행한다면 숨은 변수가 있는 세계가 숨은 변수가 없는 세계와 통계적으로 구별될 수 있음을 증명하는 영리한 수학적 이론을 제시했다. 이후 얽힌 쌍을 다룬 실험들은 일관되게 ‘숨은 변수 없음’이라는 결과를 지지했다.
어떤 유형의 거리가 얽힘을 ‘작동’케 하는가? 입자는 떨어져 있어도 얽힐 수 있기에 훨씬 놀랄만큼 떨어진 거리에서도 상관관계와 명백한 행동을 만들어낼 수 있다. 중국 연구자들은 얽힌 광자를 1천200킬로미터 떨어진 우주에서 지구로 보내는 방안을 강구해 왔다. 물리적 입자는 어떨까? 얽힘은 서로 1.3킬로미터 떨어진 전자 사이에서도 달성됐다. 전자 실험에서 인상적인 점은 전자를 광자와 얽히게 한 다음 그 광자를 전송해 다른 것과 얽히게 함으로써, 그 얽힘을 전자에게 ‘전송했다’는 것이다. 이렇게 한 뒤 전자의 상태는 임의적이지만 완벽하게 상관관계를 띤다. 이상함Spookiness은 확실히 전송할 수 있는 상태다.
의식, 다중우주, 그리고 결어긋남Consciousness, multiple universes, and decoherence
양자물리학이 사물을 아주 잘 설명했다는 점이 인정되자, 과학자들은 그들의 관심을 다른 질문으로 돌렸다. 세계가 양자라면, 왜 그리도 고전적으로 보일까? 측정에서 중첩을 무너뜨리는 게 뭐였을까? 한 가지 이론은 의식적인 존재에 의한 관찰이 측정의 핵심 특징이라는 것이다. (즉, 고양이는 상자가 열리고 실험자가 들여다보기 전까지는 살아 있는 동시에 죽어 있는 상태다.)
다른 이론은 실제로 중첩이 붕괴하지 않는다, 대신 저마다 각각의 ‘대체’ 세계가 이어진다는 것이다. 즉 측정은 붕괴가 아니라 분기branching다. 이 분기 절차는 지속적이며, 다중 세계로 간다. 이 이론들이 결합돼서 측정이 발생할 때 2개의 우주가 만들어진다, 각각의 우주에서 실험자의 의식적 생각이 내적으로 일관된 새로운 현실을 본다, 이런 아이디어도 나왔다. 다중세계 대신 다중생각many-minds이 있다는 얘기다. 이 (다소 동어반복적인) 논리에 따르면 우리가 절대 뭔가를 두 서로 다른 상태에 있는 걸로 인식하지 못하고, 의식이 뭔가를 여러 상태에 있는 것으로 인식할 수도 없어, 관찰자가 중첩된 상태와 상호작용하는만큼 여러 개별 경험을 하게 된다.
이런 이론들은 흥미롭고 SF의 친숙한 테마를 호소하듯이 포함한다. 슬프게도 이들을 증명하거나 반증하는 것은 불가능하기때문에 과학적 가치는 제한적이다. 측정 문제는 여전히 논란거리지만 결어긋남이라 알려진 현상이 중첩의 붕괴 이유에서 중요한 부분을 차지한다는 과학계의 합의가 커지고 있다. 좀 더 정확하게는, ‘붕괴’는 없고, 중첩된 양자 상태가 그 환경과 상호작용함에 따라 매우 빠르게 일어나는 결어긋남만이 존재한다. 시스템이 더 거대할수록 결어긋남이 더 빨리 일어난다. 예를 들어 단단한 진공청소기 안에서조차 태양광과의 상호작용이 먼지 입자에 10마이크로초만에 결어긋남을 일으키고, 중첩된 새끼고양이에는 10나노초만에 일으킨다. (왜 새끼고양이냐고? 슈뢰딩거의 새끼고양이는 슈뢰딩거의 고양이보다 더 작으니까!) 아무리 사고실험이라고 하지만, 새끼고양이는 숨을 쉬어야 하니까 진공청소기 속의 새끼고양이가 죽었는지 살았는지를 묻는 건 의미가 없다. 숨쉴 수 있는 환경에서 새끼고양이-결어긋남은 사실상 즉각적으로 일어나, 10-26 초밖에 안 걸린다.
육안으로 볼 수 있는 시스템일수록 더 많은 환경이 존재하므로, 결어긋남 효과가 더 커진다. 확실히 격리된 시스템조차 완벽한 격리는 불가능하기 때문에 결어긋남이 일어난다. 환경은 언제나 약간의 잡음을 일으킨다. 결어긋남 상호작용은 계산하기가 복잡하지만 수학적으로 모형화될 수 있다. 아마도 이런 복잡성 때문에 양자역학의 다른 기반이 형성된지 한참 뒤인 1991년에야 결어긋남 이론이 제안됐을 것이다.
양자정보이론Quantum information theory
양자정보이론은 양자시스템 안에서 정보가 행동하는 방식을 다루는 이론이다. 고전 정보이론의 최소단위가 0 또는 1이 될 수 있는 비트였듯이, 양자정보이론의 최소단위는 역시 0 또는 1이 될 수 있는 큐비트다. 스핀은 큐비트의 물리적으로 편리한 표현으로, 위 스핀은 0, 아래 스핀은 1이다. 편광Light polarization도 사용되는데, 수평이면 0으로 수직이면 1로 사용한다. 우리는 때때로 큐비트를 화살표로 나타내고, 그래서 0은 아래고 1은 위다.
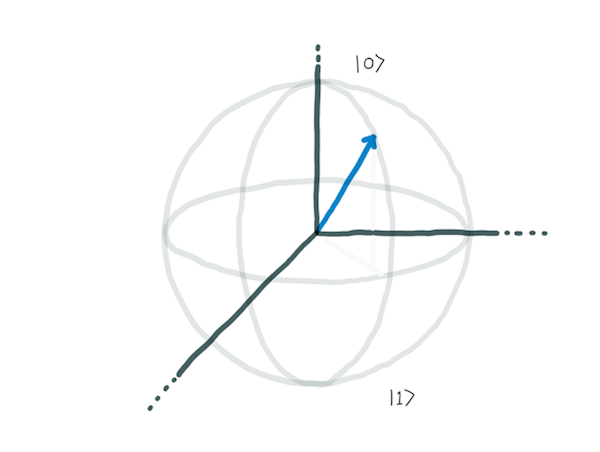
고전적인 비트와 달리 큐비트는 0과 1 상태의 결합이 될 수 있다. 이 중첩은 구체상의 한 점으로 표현된다. 단순히 0과 1사이의 확률이 아니라 구체상의 한 점인 이유는 그 중첩된 그 상태가 2차원이고 2차원 행렬로 표현되기 때문이다. 측정됐을 때 큐비트는 고전적인 0 또는 1 상태로 붕괴하지만, 측정 전까지는 멀티-큐비트-게이트를 포함한 모든 연산 명령이 더 복잡한 양자 상태에서 수행된다.
고전적인 단일-비트 논리 게이트는 비트의 상태를 뒤집는다(NOT 연산). 양자 NOT 게이트는 180도 회전을 나타내는데, 이는 구체상의 여러 다른 연산을 가능하게 한다. 예를 들어 0에 90도 회전 연산을 수행하면 큐비트를 0과 1의 중첩 상태로 만든다. (축 주위를 추가 선회하는 것으로, 이를 ‘하다마드 게이트Hadamard gate‘라 부른다.) 다른 연산은 각의 위치the angular position를 바꾸는 것(구체 주위를 감아돌리는 것)이다.
큐비트 모델이 적어도 시각적으로는 포착하지 않는 것 하나는 얽힘 개념이다. 다중-큐비트 게이트는 큐비트간의 얽힘을 만들어낼 수 있고, 그 얽힘을 풀 수도 있다. (배타적논리합exclusive-OR과 유사한) 제어반전controlled-NOT 연산이 보통 이 목적에 쓰이는데, 더 정확하게는, 얽힘이 양자 제어반전 게이트의 부작용이다. 얽힘은 시스템의 계산 능력에 큰 영향을 미친다.
얽힘은 양자컴퓨터 속도 향상의 핵심이라는 게 중론이다. 얽힘은 상태간의 상관관계를 수반하기 때문에, 얽힌 상태는 단지 두 독립된 상태의 곱으로 서술될 수 없다. 행렬 관점에서 볼 때, 얽힌 상태의 행렬은 더 작은 두 행렬로 인수분해될 수 없다. 이 기약-능력irreduce-ability은 얽힌 상태가 고전적인 컴퓨터에서 효율적으로 모사될 수 없음을 의미한다. 사실 고전적인 컴퓨터에서 대형 양자 시스템을 모사할 때 그 계산의 복잡성이 양자 컴퓨터가 월등한 계산 능력을 가질 수 있다는 사실을 일깨운 계기였다.
이 연재물의 2편에서, 우리는 계산 복잡성을 더 들여다보고, 어떤 양자 알고리즘이 그 고전적인 컴퓨터 알고리즘보다 훨씬 낮은 계산 복잡성을 띠는 방법과 이유를 설명하겠다.
저자 소개About the Author
홀리 커민스는 풀스택 개발자, 클라우드컴퓨팅 테크니컬 리드다. 단골 강연자, 자바 챔피언, 엔터프라이즈 OSGi 인 액션의 저자이기도 하다. 이 사람은 옥스포드대학교 양자계산학 박사DPhil in Quantum Computation 학위 보유자다.
—
18071x 번역 시작. 180716 인포Q 편집부의 번역 승인. 180729 초벌 번역 완료. 180731 게재. 180806 작성자의 요청에 따라 글 하단에 배치했던 저자 소개 및 저작권 표기를 최상단으로 옮김. 180912 2편 번역판 링크 추가 및 재편집. 181021 3편 번역 마무리하며 함께 재편집. 231105 저자 소개 문구의 ‘그는’을 성별 중립적인 ‘이 사람은’으로 수정함.